I wrote this ISMRM-interesting-talk review a few month ago. Today I finally got a chance to publish it on my personal website as a blog. There is no attempt to make it an exhausting review. I just listed here a few interesting talks/abstracts I found either relevant to my research or pretty cool.

Gradient-free frequency encoding imaging

Number: 1143
Authors: Sai Abitha Srinivas, Antonio D Glenn, Christopher E Vaughn, Mark A Griswold, and William A Grissom

This work experimentally demonstrates the usage of Bloch-Siegert effect in RF-gradient based frequency encoding. Bloch-Siegert effect is referring to the shift of spin precession frequency when an off-resonance RF field is applied. This effect was firstly discovered by Felix Bloch and Arnold Siegert in 1940. However, it was not introduced in MR applications until 2010. In this seminal paper, Sacolick proposed a phase-based $B_1^+$ mapping method leveraging the Bloch-Siegert effect.

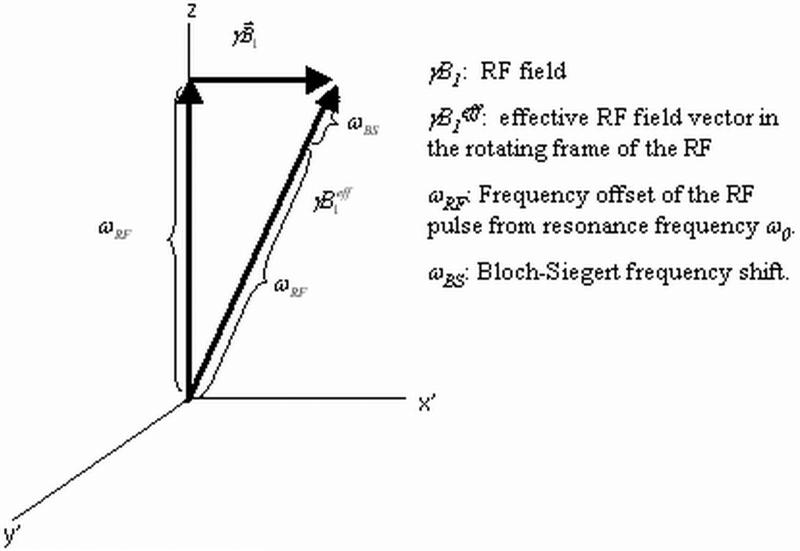
Imagine we apply an RF field that has frequency $\omega_0+\omega_{RF}$, then in the rotating frame of this RF field(Figure 1), $B_1$ will appear static while spins precess in a frequency $\omega_{RF}$. This precession frequency offset is equivalent to a static magnetic field along z axis in the RF rotating frame (Figure 1). Its vector sum with the frequency induced by the $B_1$ field is the effective $B_1$:

Under the approximation that $\omega_{RF}\gg \gamma B_1$, and the RF pulse does not excite the spins, the effective $B_1$ will appear to be still along the z axis but with an extra Bloch-Siegert component: $\omega_{BS}$:

Ignoring second-order and higher terms, we have:

By measuring the phase accrued by the BS shift, one may be able to get the magnitude of B1 map.

(TBC)